Page 125 - NUOVO_La voce della Terra_matematica4
P. 125
SPAZIO E FIGURE
L’area delle figure piane
Area del romboide e del rombo MATEMATICA
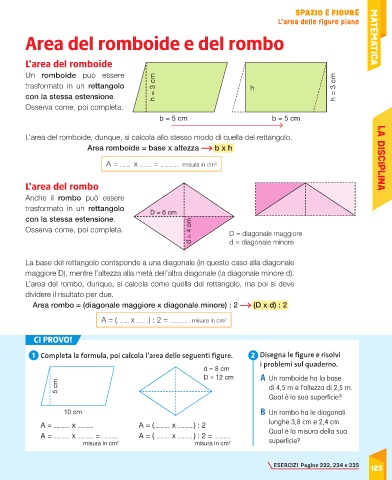
L’area del romboide
Un romboide può essere
trasformato in un rettangolo h = 3 cm h h = 3 cm
con la stessa estensione.
Osserva come, poi completa.
b = 5 cm b = 5 cm
L’area del romboide, dunque, si calcola allo stesso modo di quella del rettangolo.
Area romboide = base x altezza b x h
A = ......... x ......... = ............... misura in cm 2 LA DISCIPLINA
L’area del rombo
LA DISCIPLINA
Anche il rombo può essere
trasformato in un rettangolo D = 6 cm
con la stessa estensione.
d = 4 cm D = diagonale maggiore
Osserva come, poi completa.
d = diagonale minore
La base del rettangolo corrisponde a una diagonale (in questo caso alla diagonale
maggiore D), mentre l’altezza alla metà dell’altra diagonale (la diagonale minore d).
L’area del rombo, dunque, si calcola come quella del rettangolo, ma poi si deve
dividere il risultato per due.
Area rombo = (diagonale maggiore x diagonale minore) : 2 (D x d) : 2
A = (......... x .........) : 2 = ............... misura in cm 2
CI PROVO!
1 Completa la formula, poi calcola l’area delle seguenti figure. 2 Disegna le figure e risolvi
i problemi sul quaderno.
d = 8 cm
D = 12 cm A Un romboide ha la base
5 cm di 4,5 m e l’altezza di 2,5 m.
Qual è la sua superficie?
10 cm B Un rombo ha le diagonali
A = ............ x ............ A = (............ x ............) : 2 lunghe 3,8 cm e 2,4 cm.
Qual è la misura della sua
A = ............ x ............ = ............ A = (............ x ............) : 2 = ............
misura in cm 2 misura in cm 2 superficie?
ESERCIZI Pagine 232, 234 e 235 123