Page 97 - NUOVO_La voce della Terra_matematica5

SPAZIO E FIGURE
Il perimetro

Perimetro e formule inverse MATEMATICA

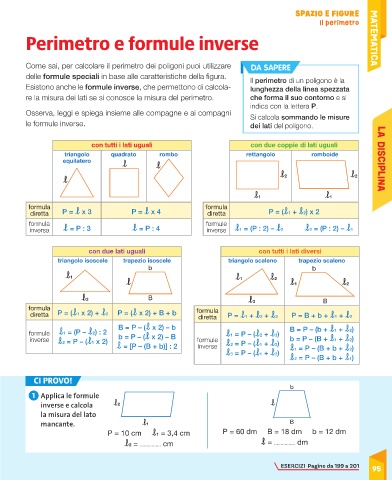
Come sai, per calcolare il perimetro dei poligoni puoi utilizzare DA SAPERE
delle formule speciali in base alle caratteristiche della figura. Il perimetro di un poligono è la
Esistono anche le formule inverse, che permettono di calcola- lunghezza della linea spezzata
re la misura dei lati se si conosce la misura del perimetro. che forma il suo contorno e si
indica con la lettera P.
Osserva, leggi e spiega insieme alle compagne e ai compagni Si calcola sommando le misure
le formule inverse. dei lati del poligono.

con tutti i lati uguali con due coppie di lati uguali
triangolo quadrato rombo rettangolo romboide
equilatero <l <l <l <l LA DISCIPLINA

<l <l <l <l 2 <l <l 2

LA DISCIPLINA
<l <l 1 <l <l 1
formula formula
<l
<l
<l
<l
diretta P = <l x 3 P = <l x 4 diretta P = (<l 1 + <l 2) x 2
formula formule
<l
<l
<l
inversa <l <l = P : 3 <l <l = P : 4 inverse <l <l 1 = (P : 2) – <l 2 <l 2 = (P : 2) – <l 1
con due lati uguali con tutti i lati diversi
triangolo isoscele trapezio isoscele triangolo scaleno trapezio scaleno
b b
<l <l 1 <l <l 1 <l <l 2
<l <l <l <l 1 <l <l 2

<l <l 2 B
<l <l 3 B
formula formula
<l
<l
<l
<l
<l
<l
<l
<l
diretta P = (<l 1 x 2) + <l 2 P = (<l x 2) + B + b diretta P = <l 1 + <l 2 + <l 3 P = B + b + <l 1 + <l 2
<l
<l
<l
<l
<l
<l
<l
formule <l 1 = (P – <l 2) : 2 B = P – (<l x 2) – b <l <l 1 = P – (<l 2 + <l 3) B = P – (b + <l 1 + <l 2)
<l
<l
<l
<l
inverse <l <l 2 = P – (<l 1 x 2) b = P – (<l x 2) – B formule <l <l b = P – (B + <l 1 + <l 2)
<l
<l <l = [P – (B + b)] : 2 inverse <l <l 2 = P – (<l 1 + <l 3) <l <l 1 = P – (B + b + <l 2)
<l
<l
<l <l 3 = P – (<l 1 + <l 2)
<l
<l <l 2 = P – (B + b + <l 1)
CI PROVO!
b
1 Applica le formule
inverse e calcola <l <l 2 <l <l
la misura del lato
mancante. <l <l 1 B
<l
P = 10 cm <l 1 = 3,4 cm P = 60 dm B = 18 dm b = 12 dm
<l <l 2 = ................ cm <l <l = ................ dm
ESERCIZI Pagine da 199 a 201 95